The network analysis of literary texts rests on a number of algorithmic foundations, which are often not sufficiently reflected in the field. In this regard, one problematic case is the existence of detached subgraphs. Here’s a classic example, the network of Goethe’s Faust, Part One (1808), visualised with our online tool ezlinavis (Faust being one of the examples you can select from the pull-down menu in the right upper corner):
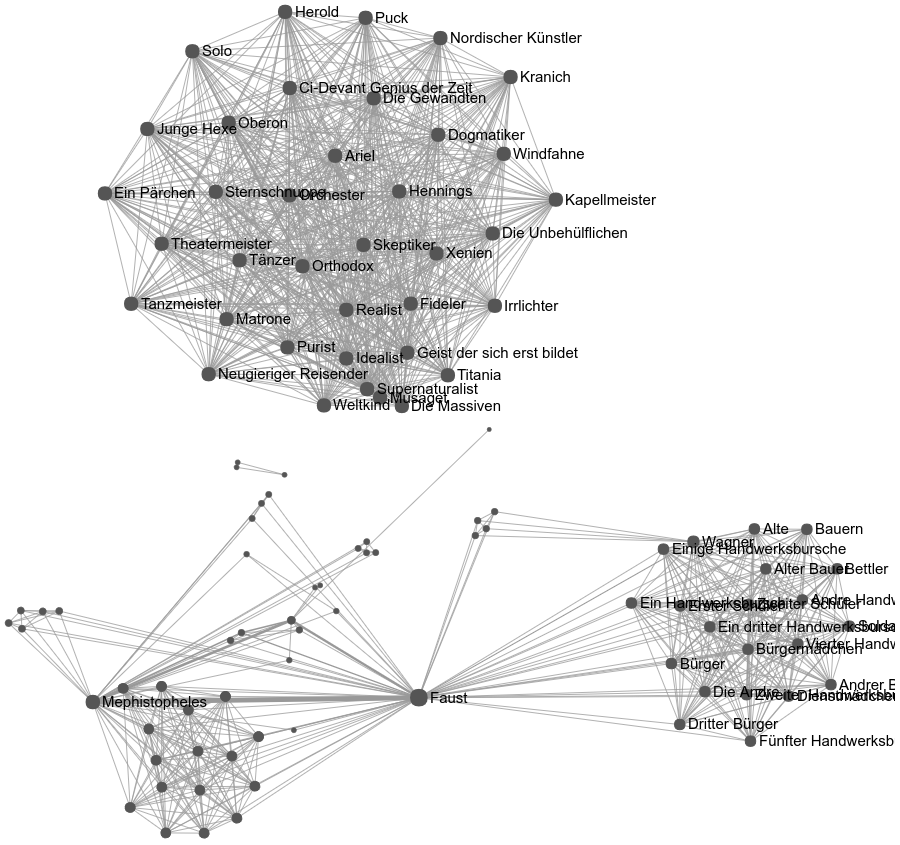
We can visually distinguish three subgraphs:
- the main graph revolving around Faust and Mephisto, which basically
comprises the entire plot of the play, except for two detached single scenes:
- Vorspiel auf dem Theater (Prelude in the Theater)
- Walpurgisnachtstraum (Walpurgis Night’s Dream)
The two latter scenes do not feature any character from the main graph, which is problematic when starting to calculate network metrics. For example, if we want to calculate the average path length, which is the average of all average distances from one node to all other nodes, how long is the distance between, say, Faust and any of the characters in the detached Walpurgis Night’s Dream? It is, well, infinite. If we still want to calculate things like the average distance, we can do that, we just have to find a way to deal with unconnected pairs of nodes. In any case: “Computing the average distance in disconnected graphs needs careful consideration.” (Zweig 2016, p. 223).
There are different ways to implement this, and even if you’re just using network tools out of the box, you should be aware of the kind of algorithm that is used to calculate network metrics in unconnected graphs.
One way is to only consider the paths that actually exist and neglect all other pairs of nodes. If we use that option, the results for six selected characters from Faust, Part One are such:
| Character | Degree | Average Distance | Closeness Centrality |
|---|---|---|---|
| Faust | 55 | 1.11 | 0.90 |
| Mephistopheles | 35 | 1.44 | 0.70 |
| Wagner | 25 | 1.71 | 0.58 |
| Margarete | 9 | 1.85 | 0.54 |
| … | … | … | … |
| Weltkind | 35 | 1.0 | 1.0 |
| Sternschnuppe | 35 | 1.0 | 1.0 |
| … | … | … | … |
This actually makes sense. Characters/speakers in Walpurgis Night’s Dream (represented by Weltkind and Sternschnuppe) are not interacting directly with characters in other scenes and “stay among themselves”, so to speak, which is why they all have an average distance of 1.0. – Yet if it is true that the central character, the protagonist if you will, is “the character that minimize[s] the sum of the distances to all other vertices” (Alberich/Miro-Julia/Rosselló 2002), we have a problem, because Faust stops being the protagonist of Faust, overrun by the 36 speakers of the Walpurgis Night’s Dream. In other words: Goethe’s Walpurgis Night’s Dream, in regard of network theory, is a link farm.
If we still want network metrics to be meaningful when it comes to determining who the central character of a play could be, we better rely on a different option. For practical reasons, the distance between two unconnected nodes is sometimes declared as length of the longest existing path, plus one. If we use this method to assume an (artificial) distance for every pair of nodes, the above table would look like this:
| Character | Degree | Average Distance | Closeness Centrality |
|---|---|---|---|
| Faust | 55 | 1.81 | 0.55 |
| Mephistopheles | 35 | 2.33 | 0.42 |
| Wagner | 25 | 2.78 | 0.35 |
| Margarete | 9 | 3.02 | 0.33 |
| … | … | … | … |
| Weltkind | 35 | 2.88 | 0.34 |
| Sternschnuppe | 35 | 2.88 | 0.34 |
| … | … | … | … |
And … Faust is back! Shortest average distance! – For our upcoming paper on the different kinds of extracting protagonists from plays, we are using this method to calculate average distances. But, having said that, it cannot be emphasised enough that since the concept of the protagonist is such a rich concept, we should not try to use but one simple measure to automatically determine such entities. Which is something we’ll address in said paper, stay tuned. 😊
Ok, let’s consider one last way to calculate distance values between unconnected
networks. E.g., when we used igraph as network library (before switching to
networkx), we saw results that were totally different, because we used a
fallback that determined that
“the length of the missing paths are counted having length vcount(graph), one longer than the longest possible geodesic in the network”
(i.e., vcount being the number of vertices of a graph). The resulting metrics,
although calculated correctly, don’t make much sense:
| Character | Degree | Average Distance | Closeness Centrality |
|---|---|---|---|
| Faust | 55 | 40.07 | 0.02 |
| Mephistopheles | 35 | 40.27 | 0.02 |
| Wagner | 25 | 40.44 | 0.02 |
| Margarete | 9 | 40.52 | 0.02 |
| … | … | … | … |
| Weltkind | 35 | 67.0 | 0.01 |
| Sternschnuppe | 35 | 67.0 | 0.01 |
| … | … | … | … |
In this approach, the assumed paths when bridging the infinite distance between two subgraphs are much longer than with the previous algorithms, and almost equal: differences in the average distances really only become visible after the decimal point. So while this approach might make sense in some contexts, it is not very helpful in our case.
All told, our maxim really has to be, and not only when confronted with subgraphs: Know your implementation!
